Определение y-параметров

Определение y-параметров

Базовые уравнения для определения параметров проводимости четырехполюсника:

I₁ = y₁₁V₁ + y₁₂V₂;

I₂ = y₂₁V₁ + y₂₂V₂.

Рис. 12.1. Четырехполюсник 

На рис. 12.1 представлен четырехполюсник с условными направлениями токов и напряжений. Проводимости в сомножителях, содержащих V₁, можно вычислить при V₂=0 из выражений:

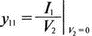
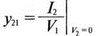
Таким образом, у₁₁ определяется как отношение I₁ к V₁ при V₂=0, а у₁₂ — как отношение I₂ к V₁ при V₂=0. Аналогично

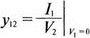
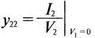
Эти y-параметры называются параметрами проводимости короткого замыкания четырехполюсника (short-circuit admittance parameters) и могут быть найдены с помощью PSpice. В качестве примера рассмотрим простую цепь, состоящую из резисторов.

На рис. 12.2 показана Т-образная схема, состоящая из трех резисторов. Чтобы найти у₁₁ и y₂₁ закоротим выход четырехполюсника (полюсы справа), обеспечив тем самым условие V₂=0. На вход четырехполюсника подадим напряжение V₁=1 В. Входной файл при этом имеет вид:

Input and Transfer Admittances

V1 1 0 1V

R1 1 2 12

R2 0 2 3

R3 2 0 6

.DC V1 1V 1V 1V

.ОРТ nopage

.PRINT DC I(R1) I(R2); для y11 and y21

.END

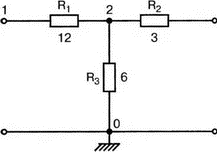
Рис. 12.2. Т-образная схема замещения 

Обратите внимание, что в команде, описывающей резистор R₂, узлы записаны в следующем порядке: 0, 2. Тем самым задается направление для тока I₂, показанное на рис. 12.3. Проведите анализ на PSpice, чтобы найти I₁ и I₂. В результате вы получите

I(R₁) = 71,43 мА и I(R₂) = -47,62 мА.

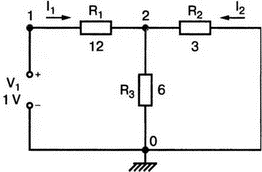
Рис. 12.3. Т-образная схема с короткозамкнутым выходом

Поскольку напряжение V₁ выбрано равным 1 В, значение I₁ численно равно проводимости у₁₁, а значение I₂ численно равно проводимости у₂₁. Следовательно,

y₁₁ = 71,43 мс и у₂₁ = -47,62 мс.

Остальные y-параметры могут быть найдены при подаче со стороны выхода напряжения V₂=1 В и при V₁=0. Последнее условие выполняется при коротком замыкании на входе. Входной файл:

Output and Transfer Admittances

V2 2 0 1V

R1 0 1 12

R2 2 1 3

R3 1 0 6

.DC V2 1V 1V 1V

.OPT nopage

.PRINT DC I(R1) I(R2); для y12 and y22 .END

Поскольку напряжение V₂ выбрано равным 1 В, значение I₁, численно равно проводимости у₁₂, а значение I₂ численно равно проводимости у₂₂. Проведите анализ и убедитесь, что

у₁₂ = -47,62 мс и у₂₂ = 142,9 мс.

Обратите внимание, что у₁₂ = у₂₁ и, следовательно, четырехполюсник является симметричным.

Отрицательные знаки для проводимостей у₁₂=у₂₁ не несут в себе какого-либо физического смысла, поскольку y-параметры не отражают свойств физических элементов. Однако легко показать, что П-образная схема на рис. 12.4 эквивалентна четырёхполюснику, описываемому y-параметрами, и поэтому она эквивалентна исходной схеме, заключенной в «черном ящике», какой бы она ни была. В нашем примере

y_а = y₂₁ + y₂₁ = 23,81 мс;

y_b = y₂₂ + y₁₂ = 95,28 мс;

y_с = -y₁₂ = 47,62 мс.

При этом реальные проводимости в схеме на рис. 12.4 положительны.

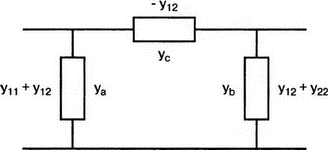
Рис. 12.4. Схема замещения для y-параметров

Если преобразовать y-параметры в z-параметры (для нашего случая в r-параметры), вычислив обратные величины, то получим z_a=42 Ом, z_b=10,5 Ом и z_c=21 Ом.

Другая схема замещения, содержащая y-параметры, показана на рис. 12.5. В ней используются два зависимых источника тока, управляемых напряжением (ИТУН/VDCS), и она следует непосредственно из исходных уравнений для y-параметров. Вспомним, что команда, предназначенная для введения во входной файл таких источников, должна начинаться с символа G.

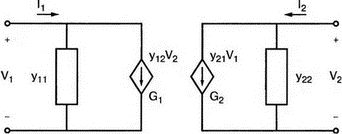
Рис. 12.5. Схема замещения для y-параметров на базе зависимого источника

Данный текст является ознакомительным фрагментом.