Низкочастотный фильтр Баттерворта второго порядка

Низкочастотный фильтр Баттерворта второго порядка

Воспользуемся таблицами нормированных многочленов Баттерворта, чтобы найти коэффициенты для фильтра второго порядка:

s? + 1,414s + 1.

Фильтр второго порядка показан на рис. 5.24. Для вводного примера найдем элементы R1, R2, R и С для фильтра Баттерворта с частотой среза fc=5 кГц. Как обычно, в качестве частоты среза принимается частота, при которой характеристика снижается на 3 дБ. Согласно теории, низкочастотный коэффициент усиления задается выражением: 

Avo = 3 – 2k,

где k представляет собой коэффициент затухания, определенный как половина коэффициента при s? из таблицы полиномов Баттерворта (см. Hillburn and Johnson. Manual of Active Filter Designs, McGraw-Hill, 1973). Для этого примера k=0,707 и

Av0 = 3 - 1,414 = 1,586.

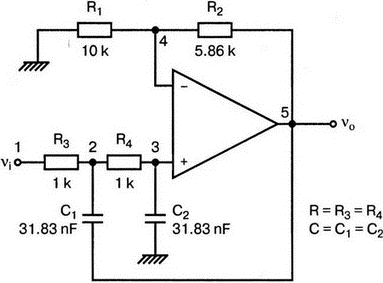
Рис. 5.24. Низкочастотный фильтр Баттерворта второго порядка 

Допустим, что R1=10 кОм. Из выражения

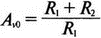
получаем R2=5,86 кОм. Если положить R=1 кОм, из выражения fc=1/(2?RC) найдем С=31,83 нФ. Чтобы проверить теорию Баттерворта, используем идеальную модель ОУ в качестве подсхемы, как показано на рис. 5.25. Для этого создайте следующий входной файл:

Second-Order Butterworth Filter

V1 1 0 AC 1mV

R3 1 2 1k

R4 2 3 1k

R1 4 0 10k

R2 5 4 5.86k

C1 2 5 31.83nF

C2 3 0 31.83nF

X 4 3 5 iop

.AC DEC 40 1 100kHz

.PROBE

.subckt iop m p vo

e vo 0 p m 2e5

rin m p 1meg

.ends

.END

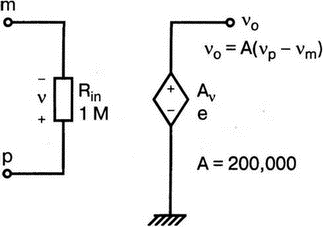
Рис. 5.25. Подсхема для идеального ОУ

Проведите анализ и получите график V(5)V(1). Выясните, что Аv0=1,586, что соответствует нашему расчету. Затем удалите этот график и получите график зависимости

20·lg(V(5)/(V(1)·1,587В)).

Убедитесь, что fc=5 кГц. Этот фильтр второго порядка должен иметь вдвое большую крутизну спада, чем фильтр первого порядка. Вспомним, что фильтр первого порядка имеет скорость спада 20 дБ/дек. Убедитесь, что при f=10 кГц Av=12,31 дБ, а при f=100 кГц Av=52,05 дБ, что составляет приблизительно 40 дБ/дек. Этот график показан на рис. 5.26.

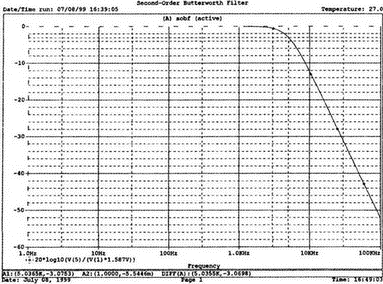
Рис. 5.26. График Боде для низкочастотного фильтра Баттерворта второго порядка

Более 800 000 книг и аудиокниг! 📚

Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением

ПОЛУЧИТЬ ПОДАРОК

Данный текст является ознакомительным фрагментом.