Годограф проводимости для последовательного RLC -контура

We use cookies. Read the Privacy and Cookie Policy

Годограф проводимости для последовательного RLC-контура

Интересная форма годографа проводимости получается для последовательного RLC-контура. Можете вы предсказать, на что она будет похожа? Если масштаб для B и G будет одинаковым, она будет окружностью. Параметры элементов в схеме, приведенной на рис. 2.25: R=50 Ом; L=20 мГн и С=150 нФ. Соответствующий входной файл:

Admittance Locus for Series RLC Circuit

V 1 0 AC 1V

R 1 250

L 2 3 20mH

С 3 0 150nF

.AC LIN 5001 1000Hz 10kHz

.PROBE

.END

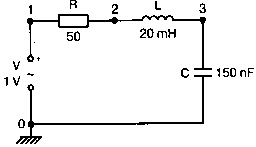
Рис. 2.25. Последовательная цепь для определения полной проводимости

Резонансная частота соответствует крайней правой точке и составляет 2906 Гц. В программе Probe необходимо выбрать Plot, Axis Settings…, на табло X Axis — User Defined, ввести значения «0А» в 20 мА, Scale Linear, затем нажать кнопку Axis Variable и для Trace Expression: набрать TR(R) и нажать OK. Выполните анализ и получите график II(R). Кривая начинается с нижней частотной границы в левой части экрана и при повышении частоты точка перемещается по часовой стрелке по овальной траектории. При перемещении с позиции 9 часов в позицию 3 часа проходится диапазон частот от 0 Гц (наш график фактически начинается при f=100 Гц) до резонансной частоты 2906 Гц. Вся нижняя половина круга приходится на диапазон от резонансной частоты до верхнего частотного предела в 10 кГц.

Распечатайте график для дальнейшего изучения. Обратите внимание, что вид графика к окружности можно менять соответствующим выбором границ на осях X и Y, хотя при этом можно потерять некоторую часть круга на экране или распечатанной копии. Этот график показан на рис. 2.26.

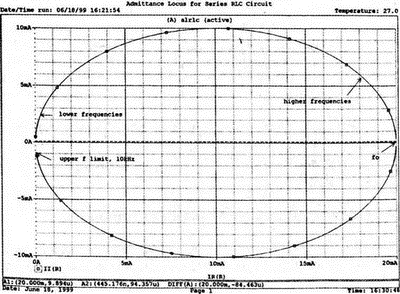
Рис. 2.26. Годограф проводимости для последовательного RLC-контура

Теперь удалите график, и выберите в качестве переменной по оси X частоту. Использование курсора для графика I(R) в функции частоты позволяет найти резонансную частоту.

Данный текст является ознакомительным фрагментом.